Un método de optimización existente para resolver los procesos programables es la optimización convexa que tiene en cuenta el tipo de función que posee el sistema, sea lineal, cuadrática y no lineal, la cual se resuelven mediante las características matemáticas, los comportamientos diferenciales y sus restricciones, teniendo en cuenta la desigualdad de Jensen, el epígrafe y la segunda derivada de cada función.
Referencias
S. Boyd and L. Vandenberghe, Convex optimization. Cambridge: Cambridge Univ. Pr., 2011.
Para resolverlo se utiliza el método del gradiente y el método de los multiplicadores de Lagrange para lograr trabajar con las restricciones de los sistemas y poderlas trabajar al interés propio, los cuales a veces pueden ser resueltos de manera analítica, por lo cual se hace necesaria la teoría y en algunos casos encontraremos aplicaciones en las que la solución se obtiene de forma más eficiente resolviendo el problema dual, diciendo que el punto óptimo debe estar lo suficientemente cerca de la marca dual, al determinar su valor óptimo y ellos son negativos o iguales a cero se llega a la condición de hoguera que traduce a una dualidad fuerte, así mismo nos deja observar la sensibilidad a las perturbaciones del sistema.
La idea es cambiar las funciones para agregarle la convexidad, a primera vista puede parecer que estamos complicando el problema porque estamos añadiendo más dimensiones al problema, pero en muchos casos esta simple transformación puede hacer que un problema inicialmente no convexo se convierta en uno que sí lo sea y por tanto se pueda resolver eficientemente, trabajando con los valores extendidos de las funciones, se puede incluir cualquier restricción de forma implícita en la función objetivo volviendo a definir su dominio, simplemente cambiando en la descripción del problema, pero esto no hace que sea más fácil de resolver.
A pesar de no haber tratado con problemas de este tipo en las aplicaciones de este proyecto, la optimización cuasi-convexa es importante en el ámbito de las telecomunicaciones porque se utiliza en una gran cantidad de aplicaciones: por ejemplo, se presenta un caso de canal bidireccional con un nodo de retransmisión en el que la asignación óptima de potencias se resuelve con un problema cuasi-convexo. En otro caso, se formula con este tipo de problemas varios ejemplos de diseño de filtros FIR (“pulso de respuesta finita”) en forma de desigualdades matriciales lineales (LMI “matriz de inecuación lineal”).
Por último, podemos ver una aplicación de control de admisión y potencia para redes cognitivas de banda ultra ancha (UWB “ultra banda ancha”), en la que se maximiza la velocidad mínima de transmisión resolviendo un problema de optimización cuasi-convexo; también se presenta una técnica para encontrar el umbral óptimo en el problema de detección con hipótesis binaria para un número arbitrario de sensores, en el que la probabilidad de error se demuestra que es una función cuasi-convexa y el problema se descompone en una serie de problemas de este tipo. En definitiva, la lista de ejemplos en los que esta variante de problemas es aplicable a la ingeniería es abundante. Esta y muchas aplicaciones se pueden encontrar en los sistemas de optimización convexa.
Por último, podemos ver una aplicación de control de admisión y potencia para redes cognitivas de banda ultra ancha (UWB “ultra banda ancha”), en la que se maximiza la velocidad mínima de transmisión resolviendo un problema de optimización cuasi-convexo; también se presenta una técnica para encontrar el umbral óptimo en el problema de detección con hipótesis binaria para un número arbitrario de sensores, en el que la probabilidad de error se demuestra que es una función cuasi-convexa y el problema se descompone en una serie de problemas de este tipo. En definitiva, la lista de ejemplos en los que esta variante de problemas es aplicable a la ingeniería es abundante. Esta y muchas aplicaciones se pueden encontrar en los sistemas de optimización convexa.
Fig. 1 Método del gradiente.
Imagen tomada de la web libre.
Referencias
S. Boyd and L. Vandenberghe, Convex optimization. Cambridge: Cambridge Univ. Pr., 2011.
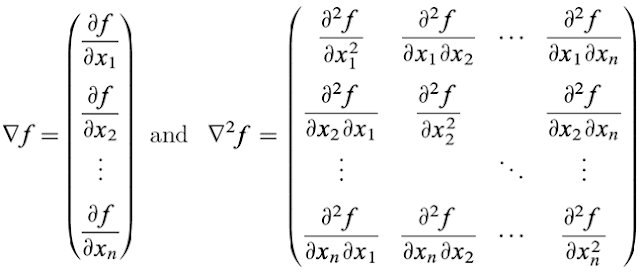
Comentarios
Publicar un comentario